TEORIA DAS ESTRUTURAS II

Δ1 = -240,50/EI
Δ1 = 135,34/EI
Δ1 = 315,10/EI
Δ1 = 53,88/EI
Δ1 = 430,70/EI
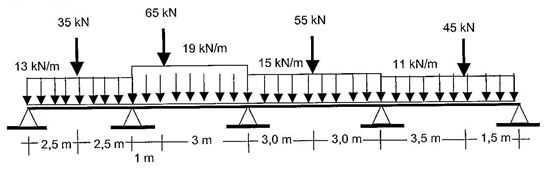
Determine, por meio do Processo de Cross o momento de engastamento Mb2, da viga abaixo. Adote uma precisão de 0,01 KN.m para os momentos e os apoios A,B,C,D e E sequencialmente da esquerda para direita.
-73,44
-37,52
86,25
65,09
61,89

Δ1 = -330,24/EI
Δ1 = -111,49/EI
Δ1 = -288,57/EI
Δ1 = -344,14/EI
Δ1 = -167,05/EI

Δ1 = - 167,05/EI
Δ1 = -344,13/EI
Δ1 = -330,24/EI
Δ1 = -288,57/EI
Δ1 = -111,49/EI
Na figura a seguir, são apresentadas quatro alternativas avaliadas na concepção de uma estrutura metálica, cujos pórticos serão compostos de perfis laminados, conectados rigidamente e engastados no apoio.

Sabe-se que, para as alternativas,1,2,3,4 a geometria dos pórticos são idênticas em relação ao comprimento e largura dos elementos, e que os carregamentos uniformemente distribuídos nos pilares têm a mesma intensidade. Além disso, considera-se um único tipo de perfil estruturas, tanto para as vigas quanto para os pilares.
Nessa condições, a relação entre os momentos fletores(M) nos topos dos pilares e nas extremidades das vigas no ponto 3 em relação as alternativas 1,2 e 4, é estabelecida por:
M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = -240,50/EI
Δ1 = 135,34/EI
Δ1 = 315,10/EI
Δ1 = 53,88/EI
Δ1 = 430,70/EI
Determine, por meio do Processo de Cross o momento de engastamento Mb2, da viga abaixo. Adote uma precisão de 0,01 KN.m para os momentos e os apoios A,B,C,D e E sequencialmente da esquerda para direita.

-73,44
-37,52
86,25
65,09
61,89

Δ1 = -330,24/EI
Δ1 = -111,49/EI
Δ1 = -288,57/EI
Δ1 = -344,14/EI
Δ1 = -167,05/EI

Δ1 = - 167,05/EI
Δ1 = -344,13/EI
Δ1 = -330,24/EI
Δ1 = -288,57/EI
Δ1 = -111,49/EI
Na figura a seguir, são apresentadas quatro alternativas avaliadas na concepção de uma estrutura metálica, cujos pórticos serão compostos de perfis laminados, conectados rigidamente e engastados no apoio.

Sabe-se que, para as alternativas,1,2,3,4 a geometria dos pórticos são idênticas em relação ao comprimento e largura dos elementos, e que os carregamentos uniformemente distribuídos nos pilares têm a mesma intensidade. Além disso, considera-se um único tipo de perfil estruturas, tanto para as vigas quanto para os pilares.
Nessa condições, a relação entre os momentos fletores(M) nos topos dos pilares e nas extremidades das vigas no ponto 3 em relação as alternativas 1,2 e 4, é estabelecida por:
M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.


-73,44
-37,52
86,25
65,09
61,89

Δ1 = -330,24/EI
Δ1 = -111,49/EI
Δ1 = -288,57/EI
Δ1 = -344,14/EI
Δ1 = -167,05/EI

Δ1 = - 167,05/EI
Δ1 = -344,13/EI
Δ1 = -330,24/EI
Δ1 = -288,57/EI
Δ1 = -111,49/EI
Na figura a seguir, são apresentadas quatro alternativas avaliadas na concepção de uma estrutura metálica, cujos pórticos serão compostos de perfis laminados, conectados rigidamente e engastados no apoio.

Sabe-se que, para as alternativas,1,2,3,4 a geometria dos pórticos são idênticas em relação ao comprimento e largura dos elementos, e que os carregamentos uniformemente distribuídos nos pilares têm a mesma intensidade. Além disso, considera-se um único tipo de perfil estruturas, tanto para as vigas quanto para os pilares.
Nessa condições, a relação entre os momentos fletores(M) nos topos dos pilares e nas extremidades das vigas no ponto 3 em relação as alternativas 1,2 e 4, é estabelecida por:
M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = -330,24/EI
Δ1 = -111,49/EI
Δ1 = -288,57/EI
Δ1 = -344,14/EI
Δ1 = -167,05/EI

Δ1 = - 167,05/EI
Δ1 = -344,13/EI
Δ1 = -330,24/EI
Δ1 = -288,57/EI
Δ1 = -111,49/EI
Na figura a seguir, são apresentadas quatro alternativas avaliadas na concepção de uma estrutura metálica, cujos pórticos serão compostos de perfis laminados, conectados rigidamente e engastados no apoio.

Sabe-se que, para as alternativas,1,2,3,4 a geometria dos pórticos são idênticas em relação ao comprimento e largura dos elementos, e que os carregamentos uniformemente distribuídos nos pilares têm a mesma intensidade. Além disso, considera-se um único tipo de perfil estruturas, tanto para as vigas quanto para os pilares.
Nessa condições, a relação entre os momentos fletores(M) nos topos dos pilares e nas extremidades das vigas no ponto 3 em relação as alternativas 1,2 e 4, é estabelecida por:
M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = - 167,05/EI
Δ1 = -344,13/EI
Δ1 = -330,24/EI
Δ1 = -288,57/EI
Δ1 = -111,49/EI
Na figura a seguir, são apresentadas quatro alternativas avaliadas na concepção de uma estrutura metálica, cujos pórticos serão compostos de perfis laminados, conectados rigidamente e engastados no apoio.

Sabe-se que, para as alternativas,1,2,3,4 a geometria dos pórticos são idênticas em relação ao comprimento e largura dos elementos, e que os carregamentos uniformemente distribuídos nos pilares têm a mesma intensidade. Além disso, considera-se um único tipo de perfil estruturas, tanto para as vigas quanto para os pilares.
Nessa condições, a relação entre os momentos fletores(M) nos topos dos pilares e nas extremidades das vigas no ponto 3 em relação as alternativas 1,2 e 4, é estabelecida por:
M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

M3= M4= M15= M16< M7= M7.
M7= M8< M3= M4< M15= M16.
M3= M4= M7= M8= M15= M16.
M15= M16< M7= M8< M3= M4.
M7= M8< M15= M16< M3= M4.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = 164,11/EI
Δ1 = 53,74/EI
Δ1 = 749,04/EI
Δ1 = -402,56/EI
Δ1 = -167,20/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 6 EI ; Trecho BC = 3 EI ; Trecho CD = 2EI ; Trecho BE = 4EI ;Trecho CF = EI.

Δ1 = 749,04/EI
Δ1 = -167,20/EI
Δ1 = 53,74/EI
Δ1 = -402,56/EI
Δ1 = 164,11/EI